AdvancedResearch
Monotonic-Solver 0.5 Released
by Sven Nilsen, 2020
A new version of the Monotonic-Solver has been released (V0.5).
The Monotonic-Solver library is currently being used in AI safety research, to generate graphs of example problems like this one:
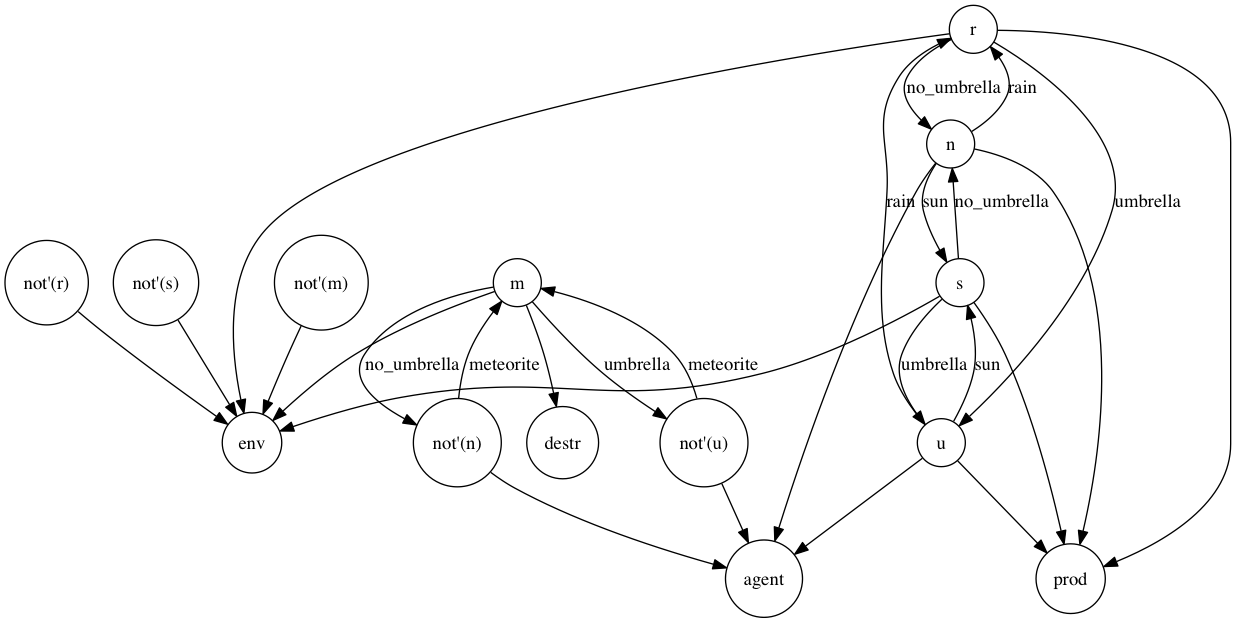This is an introduction example to Cartesian Frames (Chu-spaces) to model semantics of Agents vs Environments.
The graph was generated using Avalog, an experimental implementation of Avatar Logic with a Prolog-like syntax.
Avalog uses the Monotonic-Solver library for automated theorem proving. For a formal introduction to Avatar Logic, see Summary of Avatar Extensions.
In this blog post I will give a short introduction to monotonic solving, what is new in this version, and why it is important for Avalog.
Generic Automated Theorem Proving
The Monotonic-Solver library is a generic automated theorem prover.
An automated theorem prover is a program that proves e.g. a mathematical theorem. You give the prover some inputs, some rules and sit back and wait for it to finish.
Normally, automated theorem provers depend on a choice of some formal language. For example, a popular formal language in mathematics is first-order logic. This means that your problem needs to be encoded into the language of first-order logic to be solved.
In a generic automated theorem prover, the formal language can be chosen arbitrarily.
Basically, you can invent your own language, for example to:
- Generate outlines of fictional story plots
- Use the automated theorem prover as intelligent mind mapping software
- Organize knowledge e.g. about Category Theory
There are many uses of automated theorem provers outside mathematics.
Monotonic Solvers
A monotonic solver has a constraint that any fact being inferred from knowledge can not be deleted later.
Basically, a monotonic solver is like an elephant: It never forgets!
That is the only assumption!
Considering how small this assumption might look, it is actually a very big deal when solving problems:
- It is not good for e.g. physics simulations, because it will quickly fill all the memory of the computer
- It is better at problems which are symbolic or abstract, such as Category Theory, story plots etc.
What’s New in 0.5
In previous versions, when the solver ran into the maximum proof size limit, it only reported an error, which was the same when the goal was unreachable.
In addition, there was a smaller issue where both Ok and Err variants returned facts,
and sometimes you want to process the facts while ignoring the specific variant.
V0.5 has redesigned the result from:
Result<Vec<T>, Vec<T>>
to:
(Vec<T>, Result<(), Error>)
Another change was support for an acceleration data structure.
Why Acceleration Data Structure is Important for Avalog
Avalog builds an index of sub-expressions to reduce worst-case performance.
Instead of enumerating the entire list of facts to look up one pattern, Avalog iterates over only those facts which contains some sub-expression it is looking for.
For example, this code has worst-case performance O(N^2) where N is the number of facts:
for e1 in facts {
if let Rel(a1, b1) = e1 {
for e2 in facts {
if let Rel(a2, b2) = e2 {
if a2 == a1 { ... }
}
}
}
}
An index of sub-expressions reduces this to O(N * M + N) where M << N (M is much smaller than N).
build_index(); // <--- builds index before inference rules
for e1 in facts {
if let Rel(a1, b1) = e1 {
for e2 in find(a1) { // <--- only look up facts that contains `a1` as sub-expression
if let Rel(a2, b2) = e2 {
if a2 == a1 { ... }
}
}
}
}
Using an index of sub-expressions is a trade-off between flexibility and performance. There are many variants of expressions in Avalog, so using a common index simplifies maintenance.
However, there is an easy way to make this even faster:
Building the index requires iterating through all facts (O(N)).
Here, one can exploit the property of monotonic solvers. Since no facts are deleted, it means only new facts need to be iterated through when building the index. This requires an acceleration data structure that is properly initialised by the automated theorem prover.
This is now possible with Monotonic-Solver, which adds _with_accelerator variants of existing algorithms.
Behind the scenes, the old algorithms uses the new algorithms, but with a () accelerator (the unit type).
The interface for inference rules has also been redesigned.
HashSet cache and cache_filter arguments are now replaced with a solver: Solver<T, A = ()>.
The accelerator is accessed using solver.accelerator.